El Problema de Transporte se aplica a las matemáticas y la economía
El problema de transporte es un caso particular de problema de programación lineal en el cual se debe minimizar el coste del abastecimiento a una serie de puntos de demanda a partir de un grupo de puntos de oferta -posiblemente de distinto número-, teniendo en cuenta los distintos precios de envío de cada punto de oferta a cada punto de demanda.
En el ejemplo siguiente se busca encontrar el número de unidades a enviar desde cada fábrica a cada cliente minimizando el coste total.
Formular el Modelo
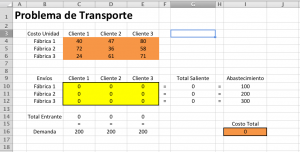
El modelo que vamos a resolver se muestra a continuación en Excel.
1. Para formular el problema de transporte debemos responder a las siguientes preguntas:
a. Cuáles son las decisiones a tomar? Para este problema, necesitamos que Excel encuentra cuantas unidades se deben enviar desde cada fábrica a cada cliente.
b. Cuáles son las restricciones para estas decisiones? Cada fábrica tiene un capacidad de suministro fijo y cada cliente tiene una demanda fija.
c. Cuál es la medida general del rendimiento de estas decisiones? La medida general del rendimiento es el costo total de los envíos, por tanto el objetivo es minimizar esta cantidad.
2. Para hacer el modelo más fácil de entender, daremos nombre a los siguientes rangos.
| Nombre Rango | Celdas |
|---|---|
| CostoUnidad | C4:E6 |
| Envios | C10:E12 |
| TotalEntrante | C14:E14 |
| Demanda | C16:E16 |
| TotalSaliente | G10:G12 |
| Abastecimiento | I10:I12 |
| CostoTotal | I16 |
3. Inserte las siguientes funciones.
| Celda | Función |
|---|---|
| G10 | =SUMA(C10:E10) |
| G11 | =SUMA(C11:E11) |
| G12 | =SUMA(C12:E12) |
| C10 | =SUMA(C10:C12) |
| D10 | =SUMA(D10:D12) |
| E10 | =SUMA(E10:E12) |
| I16 | =SUMAPRODUCTO(CostoUnitario,Envios) |
Explicación:
- Las funciones SUMA calculan el total enviado de cada fábrica (Total Saliente) para cada cliente (Total Entrante). El Costo Total es igual a SUMAPRODUCTO (1) de CostoUnitario y Envios.
Prueba y Error
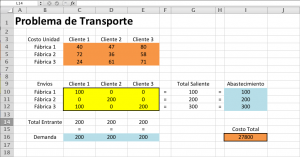
Con esta formulación se vuelve fácil analizar cualquier solución probable.
For ejemplo, si enviamos 100 unidades desde la Fábrica 1 al Cliente 1, 200 unidades de la Fábrica 2 al cliente 2, 100 unidad es desde la Fábrica 3 al Cliente1 y 200 unidades desde la Fábrica 3 al Cliente 3, el Total Saliente es igual al Abastecimiento y el Total Entrante es igual a la Demanda. La solución tiene el costo total de 27800.
No es necesario usar prueba y error. Ahora describiremos cómo usar Solver para encontrar rápidamente la solución óptima.
Solucionar el Modelo
Para encontrar la solución óptima, ejecute los siguientes pasos.
1. Click en la pestaña Datos, click en Solver. Si no puede ver el botón Solver seleccione Herramientas, Complementos y click en Solver.Xlam. Ingrese los parámetros de Solver:
2. Ingrese CostoTotal como Objetivo.
3. Click en Min (minimizar).
4. Ingrese Envios en Cambiando las Celdas de Variables.
5. Click en Agregar para ingresar la siguientes restricción:
TotalEntrante = Demanda
6. Click en Agregar para ingresar la siguientes restricción:
TotalSaliente = Abastecimiento
7. Check en Hacer Variables Sin Restricciones No Negativas. y seleccione Simplex LP
8. Finalmente, click en Resolver
Método de Solución: Simplex LP
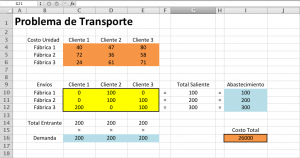
La solución óptima:
Conclusión:
- Es óptimo enviar 100 unidades de la Fábrica 1 al Cliente 2, 100 unidades de la Fábrica 2 al Cliente 2, 100 unidades de la Fábrica 2 al Cliente 3, 200 unidades de la Fábrica 3 al Cliente 1 y 100 unidades de la Fábrica 3 al Cliente 3. La solución da un costo mínimo de 26000. Todas las restricciones están satisfechas.
Enlaces:
Video:
Notas:
- (1) La función SUMAPRODUCTO permite sumar varios componentes de una matriz previamente identificados y multiplicados, o dicho de otra forma, permite multiplicar rangos de una base de datos y luego sumar su resultado según los criterios asignados.
- En su manera sencilla, esta función se puede aplicar para averiguar cuáles fueron las ventas de un producto X en un mes determinado conociendo el precio de los productos y el número de productos vendidos.